This book develops and defends a view of propositions as structured entities, very like sentences, having constituents arranged and unified in a certain way. Both Frege and Russell held such a view, and the problem of the unity of the proposition has a long lineage in the history of philosophy.[1] But King's approach is fundamentally a-historical, though he devotes a chapter to the views of Frege and Russell. There is no discussion of Kant on the unity of the proposition, for example. On the other hand, Frege himself developed his doctrine of saturated/unsaturated entities completely a-historically, with no mention, as far as I know, of Kant in particular. It might be supposed that this otherwise regrettable lack of rapprochement with the history of philosophy is justified in this case by the fact that the historical discussion did not have the benefit of Frege's and Russell's logic. But King does not make much use of modern logic in developing his doctrine regarding the unity of the proposition, save for the fundamental notions of an n-place relation, sentential connective, function, etc. Frege and Russell -- Russell especially -- are another story, however, as we'll see.
This view of propositions contrasts sharply with the idea, defended subtly and ably by Stalnaker[2] and others,[3] that propositions are sets of possible worlds; or the idea, developed by Barwise and Perry,[4] that they are sets of situations (which themselves may have structure and may be partial or even impossible).[5] Or one can start with propositions as primitive and build worlds or situations out of them, even allowing for partiality and impossibility. But King, in a mere footnote (p. 3), citing an argument of Soames, rejects any such approach without, however, rehearsing Soames' argument -- as if its conclusion is foregone. I note that research in both Montague Grammar and Situation Theory proceeds apace, despite Soames' alleged refutation.[6]
In fact, the structured propositions view faces a difficulty far more profound than Soames' complaint.[7] For as Russell shows in Appendix B of Principles of Mathematics, any such theory is very likely inconsistent, unless considerable care is taken to work out the identity and existence conditions for propositions. None other than the great logician Alonzo Church wrote a seminal paper about this, and the prominent philosopher David Kaplan has published a paper on it (well, related to it).[8] But it does not seem to be well known or properly appreciated by members of the structured Russellian propositions (SRP) group (Richard, Soames, Salmon, King, etc; see below.). The basic unanswered question is this: What is the fundamental logical background to the theory of Russellian propositions? Russell and Church took it to be the ramified theory of types. But the SRP does not appear to have addressed the question explicitly.[9]
King's book is divided into seven chapters and an appendix, with a subject index. It is quite well written, in keeping with contemporary philosophy of language, which in general suffers from a lack of rhetorical and polemical sharpness. (Think of Reid, Frege, Russell, Quine, Prior, Ryle, Kaplan, even, if not often, Kripke and Salmon, and compare their writing to the writing of the SRP’s members.) One feature of King's approach is very admirable: He cares that he is understood. So instead of choosing absolute precision and generality, he chooses to be understood, leading one through his theory very lucidly, always focused on the reader's comprehension.
The "Introduction" (Chapter 1) is revealing. King is concerned to reply to "recent" criticisms of propositions in general and structured propositions in particular. And he is focused on how his own theory can deal with these objections. That is apparently why he organizes the chapters of the book as he does. First comes some discussion of Russell and Frege, then his own theory, objections to the theory, and only after that objections to structured propositions and to propositions in general. The last two chapters address the issues of propositional attitudes and the paradox of analysis. In this review I will focus mainly on chapters 1-3, which contain the essence of King's contribution, and only briefly on the remainder, which consists of applications of theory.
In Chapter 1, King states the primary question -- which is the question of the unity of the proposition: What is it that "holds together the constituents of propositions and imposes structure on them?" (p. 9) King rejects the idea that structured propositions are, or are represented by, n-tuples, e.g., that the proposition that Annie likes Carl is or is represented by, the triple <Annie, liking, Carl>.[10] He wonders why the triple <liking, Annie, Carl> wouldn't do as well. So there is a "Benacerafian" problem. (Why pick one tuple, rather than the other? So pick none.) This problem has never impressed me very much. As Quine says of numbers: "The subtle point is that any progression will serve as a version of number as long and only as long as we stick to one and the same progression: There is no saying absolutely what the numbers are; there is only arithmetic."[11] Likewise, an n-tuple account of propositions may well work out, so long as we stick to one account. There may be no saying absolutely what propositions are; there is only our discourse. Although King tries to say what propositions are absolutely, his view is itself either highly ontologically obscure or else, I believe, subject to the same "Benacerafian" worry. (See below.)
In his discussion of Frege, King focuses on the saturated/unsaturated metaphor, and certain confusions (or changes of mind?) that may be found in the post-Grundgesetze essays and correspondence. For example, Frege appears to waffle on the question whether not, not A expresses the same proposition as A. Since King's concern is with the problem of unity, it is natural for him to focus on the saturated/unsaturated entities distinction -- which Frege himself regards as a metaphor, and one which gives us only "hints." And King is right to wonder about the meaning of the metaphor. But the post-Grundlagen, pre-Grundgesetze essays, wherein Frege introduces the metaphor, contain a wealth of notions and distinctions, most of which are now fundamental to logic, that serve to motivate the metaphor. It seems to me counterproductive to focus on the metaphor but not its motivation. In "Function and Concept," for example, Frege is concerned to point out that the 'x' in, say, f(x) = x2 is not "part of the function." To represent the expression of the function itself, we need gaps, as in f( ) = ( )2; and he is concerned to distinguish the function itself from its expression on the one hand, and its graph -- or "course of values" -- on the other. To this day, mathematicians do not have an "official" explanation of why, say, x2 - 4x = x( x - 4) is significant, but x2 - 4x = x2 - 4x is not. Frege's explanation is that while the functions represented in the first equation are the same (since they have the same values for the same arguments), when values for the variables are supplied, the result is two expressions denoting the same number but differing in sense. I should add that King tries to deal with a related issue in his chapter on the paradox of analysis (Chapter 7). But the problem just noted seems to me to be even more fundamental than the paradox of (philosophical) analysis, since it has to do with the meaning of mathematical statements for mathematicians. We like to think of mathematics as purely extensional. But it seems it can't be. This problem, through Salmon's influence, has come to be known as "Frege's Puzzle" since it is essentially the problem raised at the beginning of "On Sense and Reference." Mathematicians and logicians need to realize that it is not an isolated problem in the philosophy of language, but is endemic to our understanding of mathematics itself. I simply don't see how King could have ignored it.[12]
Finally, I would add that one of Frege's most important contributions to our understanding of the logical form of propositions seems to me to run contrary to the Chomskyan conception of LF (logical form). Frege, combating the school grammar conception of subject and predicate, analyzed concepts as functions (to truth values). But Chomsky's LF has, it seems, reintroduced the old notion, and with it the old confusions concerning logical form. Take a look, as a case in point, at King's examples 3 and 3a on p. 29 and consider how those sentences might be rendered in modern logical notation.
As for Russell, King deals mainly with Chapter IV of Principles, "Proper Names, Adjectives, and Verbs." Here Russell makes a number of obscure claims and arguments and King doesn't hesitate to pounce on them. For example, Russell claims that every assertion contains exactly one verb, and King gives a conjunction of sentences with two verbs as a counterexample. But I think a far more generous interpretation is to take Russell's claim to be about closed atomic sentences. Likewise, King complains at length about Russell's claim that in the case of intransitive verbs, as in "Smith breaths," we have an assertion of "a definite relation to an indefinite relatum." Here Russell seems to be making the innocent point that "Smith breaths" is short for "Smith breaths something." But King finds something wrong in this, and I confess that I have not been able to follow King's argument on this score. There is one remarkable Russellian obscurity that King does not mention. It concerns Russell's notion of a "term." It's well known that the Russell of Principles held that any object of thought is a term, whether existent or not, including men, moments, and chimeras. But a bit later (after making this assertion) Russell declares that terms are "indestructible." Whatever may be the case with moments and chimeras, men are not indestructible! Russell is notorious for lapsing into use/mention confusion; and perhaps this is an instance of it.
Russell raises the problem of the unity of the proposition by noting, several times over, that 'Caesar died' forms a unity that may be judged true or false, whereas 'Caesar's death' does not, and that the difference seems to lie in the "active" use of the verb 'to die'. But he adds "I do not know how to give a clear account of the distinction." From what Russell does say, however, King concludes that "we seem to get a collapse of true propositions into the facts that make them true. This of course also means that there are no false propositions." (p. 23) I don't see the "of course." We can define the proposition expressed by 'Caesar didn't die' to be the one which is false if and only if 'Caesar died' is true. Nevertheless, King may have in mind a more elaborate truth-maker argument. It's just not clear from the relevant passage what that argument is.
At the end of Chapter IV, Russell writes: "I shall proceed in the next two chapters, to discussion arising out of consideration of adjectives, to topics connected with verbs." In a fuller discussion of Russell's views on propositions, these chapters would have to be taken into account. In general, as Russell says here, adjectives correspond to class terms, whereas verbs correspond to propositional functions. We thus have something roughly akin to the modern distinction between a monadic and a polyadic predicate. The distinction is highly significant, of course, since for one thing, monadic predicate logic is decidable, but polyadic predicate logic is not.
The most glaring fault in King's historical discussion of Russell's views on propositions in Principles, is the lack of any mention of Russell's Paradox of Propositions (as I will call it; and it is not to be confused with Russell's Paradox) set forth in Section 500 (Appendix B). It was this contradiction that led Russell to abandon the simple theory of types in favor of the ramified theory, with all that entails, e.g. the need for the axiom of reducibility. Here is Russell's argument, as formulated by Alasdair Urquhart, which closely follows Russell's original:
If m is a class of propositions, then the proposition (p) (p ∈ m ⊃ p) asserts that all propositions in m are true. This proposition itself can be either a member of the class m or not. Let w be the class of all propositions of the above form that are not members of the pertinent class m; that is,
w = {q: (∃m) [(q = (p) (p ∈ m ⊃ p) . q ∉ m]},
and let r be the proposition (p) (p ∈ w ⊃ p). Then if r ∈ w, it satisfies the defining condition; hence, there is a class of propositions m so that r is identical with the proposition q = (p) (p ∈ m ⊃ p). But since r is identical with this proposition, it follows that the constituents of r are identical with the corresponding constituents of q, so that m = w. Hence, r ∉ w. Conversely, if r ∉ w, then by its definition, it satisfies the condition defining w, so that r ∈ w. Thus we have derived a contradiction.[13] [14]
As Urquhart observes, crucial to this derivation is the inference that m = w, from the assumption that the propositions mentioning them (as indicated above) are identical. That is, it appears that the structured view of propositions is especially vulnerable to this contradiction. The essential assumption is that if a and b are distinct objects, then the propositions having them as constituents differ.[15] This is not true of possible worlds semantics, since e.g. the propositions expressed by "Jones wears a hat or he doesn't" and "Smith wears a hat or he doesn't" will express the same proposition whether or not Smith and Jones are identical.[16]
As one might expect, after examining the foregoing argument, King's theory falls prey to this same contradiction, though an extra premise or two is needed to show that, by King's own lights, the diagonal proposition, r, exists; but I daresay King is not alone. (See below.)
Turning now to King's theory, King presents it so simply and economically that it is easy to summarize. King works within a "minimalist" Chomskyan framework. So there is the distinction between the surface sentence and the LF level (the level of "logical form"). The syntactic structure of sentences is analyzed semantically in terms of the LF representation. According to King, the structure of the proposition expressed by 'Rebecca swims' is given by the diagram (4b, p. 30):
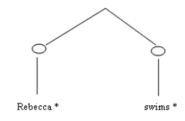
Here the branching lines represent the "sentential relation," R, holding between 'Rebecca' and 'swims' at the LF level.[17] The vertical lines are the semantic relations 'Rebecca' bears to Rebecca (Rebecca*) and that 'swims' bears to the property of swimming (swims*). The ovals are the relation between properties of joint instantiation of properties of words. The word 'Rebecca', for example, jointly instantiates the properties of (a) referring to Rebecca (Rebecca*), and (b) occurring at the left terminal node in R such that 'swims' occurs at the right terminal node and has the property of swimming as its semantic value.
King summarizes his view thus:
The relation obtaining between Rebecca* (Rebecca) and the property of swimming that binds them together in the proposition 4b is the following: There are words in some language occurring in the sentential relation R as follows:
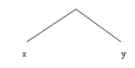
such that x has its semantic value ___, and y has its semantic value … . Rebecca stands in this relation (and occupies the spot ___) to the property of swimming (which occupies the spot … ). Roughly, this relation, which I claim holds Rebecca and the property of swimming together in the proposition that Rebecca swims, results from composing the sentential relation R with the referring/expressing relations between 'Rebecca' and Rebecca and 'swims' and the property of swimming, while existentially generalizing away the words 'Rebecca' and 'swims'. (p. 31)
King adds in a footnote that for complete generality we have to existentially generalize the language parameter as well.
King claims at least two advantages of this account: First, it makes it obvious that propositions exist; and secondly, it makes it clear how propositions "represent" the world. I don't think that either of these claims is obviously true, and there are other difficulties as well.[18]
First, it is King's view that propositions are not mathematical objects (for the Benacerafian reason -- which entails, if you think about it, that nothing whatever, given pretheoretically, is a mathematical object!). But the diagrams he employs in order to display the structure of a proposition must be mathematical objects; they are graphs of a certain kind (as in "graph theory"). So he certainly cannot identify the diagram with the proposition whose structure it displays. This raises all over again the question of what propositions are. I myself would be content, others things being equal, to identify the proposition with its diagram, qua mathematical type. But King does not have this option. So the question to which King's book is devoted remains open: What are propositions?
Secondly, King never tells us what a language or a sentence of a language is ontologically. There are hints that King's view is that languages (natural languages) and their sentences are empirically given phenomena, occurring in the actual world. So there is no more problem about their existence than there is about the tree in my front yard. But there is still a problem for King's view. Given that a language, such as English, is productive, that is, given knowledge of the finite lexicon, one can produce a sentence never produced before. Since propositions, on King's account, are tied to sentential relations, it is not clear how this productivity is possible. One would have thought that first one has the thought, or "entertains" the proposition, and only then one tries to put it into words. But for King, until the words are out, the proposition doesn't exist. So, should we conclude that we can "entertain" non-existent propositions? Of course, the view that propositions are pre-linguistic, contrary to King's view, may seem to put propositions back on the dark side; but one bit of evidence that they are indeed pre-linguistic is the fact (admittedly disputable) that animals, dogs, say, can have propositional thoughts. To put the point more neutrally and critically of King's theory: the theory entails that dogs can't think propositionally; and that closes a door a priori that should remain open for empirical reasons.
Thirdly, King simply assumes that there are properties and relations, but has nothing to say about what they are. Those who think that propositions are obscure entities are likely to think the same of properties and relations. Quine did. For him the only reality was linguistic behavior. Given this, it is hardly obvious as King insists it is, that propositions in his sense exist, since it's not obvious what properties and relations are, and hence not obvious that they exist. Furthermore, propositions can be readily thought of as properties -- properties of the actual world (or of worlds in general) or even properties of truth values.[19]
King might protest that, unlike properties and relations, which simply hold (or don't) of the world, propositions represent it. I find this a very peculiar idea -- but very common in the literature -- as if propositions were symbols or pictures (as are sentences), whereas properties and relations are non-representational aspects of reality. But when I believe that G. W. Bush is President of the U.S.A., I believe that this fact is a property of the actual world. That is, I believe that the actual world has the property that G. W. Bush is currently President of the U.S.A. Perhaps one will complain that I am confusing the proposition with the fact that makes it true. But I think that itself is a confusion. We don't represent the world by means of propositions, we describe it, or state what it is like. As producers of propositions, we are not like painters; we are more like plumbers. A plumber who believes that your water lines are clogged, will try to fix it, not because he stands in the believes relation to some representation, some sort of picture of the state of your water lines, but because he believes that reality has the property that your water lines are clogged.
Finally, as I said above, I believe that King's theory is subject to Russell's Paradox of Propositions, and hence is inconsistent. The relevant sentence occurs in a number places, e.g. above, and in Urquhart's article and there is another version of it in Church's article, not to mention Russell's own. So the relevant sentential relation and Chomskyan tree (or the bracket version) exists. That's enough to show that King's theory, or any theory meeting Russell's criterion -- that if a and b are distinct objects then the propositions mentioning them are distinct -- falls prey to this contradiction.[20] Thus, likewise, Kaplan's theory set forth in his famous paper "Demonstratives" is inconsistent, as is much subsequent theorizing by Salmon, Soames, Richard, Perry, Braun, and many others. The philosophy of language needs a coherent background logical theory that these philosophers have not, it seems, thought about, much less formulated. Kaplan, I believe, may be old fashioned enough to insist that, like Church, the ramified theory of types is what is needed.[21] But younger philosophers may want to seek a new solution.[22] In any case, my point here is that there is no longer, and in fact there was never, any excuse whatsoever to ignore the problem. Time's up.[23]
Let me now turn to King's Chapter 3 in which he replies to the objections he chooses to reply to -- in particular, not the ones mentioned above about animal thoughts and propositions as properties of the world. According to King, propositions came into existence with the advent of language and did not exist prior to that, and so, although things were "a determinate way" pre-linguistically, nothing was true or false, since the bearers of truth and falsity did not exist. King does not develop this distinction -- between things being a determinate way in the past, and its being true, then, that things were that determinate way -- but it would seem to be a natural consequence of the view that propositions, like (some) paintings, are representational in nature. Just as paintings did not exist before painters and paint, so with propositions. But in the case of propositions, this seems to me to be a distinction without a difference. We need not think of propositions as representational at all. We can think of them simply as properties that hold or do not hold of the world.
All this gets King into a tangle of unwieldy distinctions over the analysis of true modal claims such as "It is possible that there should have been no life." The issues involve what is true and what is not, in the view, originally proposed by Plantinga,[24] known as "serious actualism" -- the view that objects that don't exist at a world have no properties there, including the property of not existing there, and the property, in the case of propositions, of being true there. (King appears to be a serious actualist.) But ultimately the issues stem from a general problem (not apparently well understood or recognized by the SRP group) concerning contingency and modal logic first observed by Prior.[25] It is that it is not at all easy to reconcile modal logic with contingency, since the combination of just about any normal modal logic (i.e. one having the rule of necessitation) and classical quantification theory, allows the derivation of a formula that (interpreted naturally) asserts that every object is a necessary existent. All this was discussed in great detail in rather important papers from the early nineties by Christopher Menzel, Bernard Linsky, Edward Zalta, and myself.[26]
As King notes in his final objection and reply, on his view '1 = 2' and '2 = 1' express different propositions, and some might find this view implausible. Likewise 'Snow is white' and 'Schnee ist weiss' express different propositions. King, however, makes a case for it based on work of Richard. (See King's book for the references.) But making a case for it is not, in my opinion, enough. Perhaps the most fundamental role played by propositions, and the one we advert to when introducing the notion (in, say, courses in elementary logic), is that of explaining translation. What do 'Snow is white' and 'Schnee ist weiss' have in common? Well, they express the same proposition.[27] [28]
In the last two chapters King defends the view that propositions vary in truth value with respect to possible worlds, but not with respect to more "local" parameters, such as place and time (contrary to the view of, e.g. Montague Grammar), and he "solves" the paradox of analysis by appeal to the super fine-grainedness of his propositions. There is then an appendix on quantification. (See n. 28.) I've already mentioned that King has missed the opportunity to defend his view by showing that it has a way of dealing with Frege's Puzzle; and I have commented that this puzzle arises not merely within philosophy, but within mathematics itself -- a point not often noted, especially by mathematicians. As for the issue of variation in truth value: What is abundantly clear is that allowing variation with respect to one truth value determining parameter, but not others, that seem to function similarly, is certainly inelegant; and it is equally abundantly clear that sentences, including propositional attitude reports, can vary in truth value with respect to local parameters. The idea that the propositions don't vary in truth value, coordinately, simply makes them even more of a mystery.
I would recommend King's book to anyone who wants to know where King's School of philosophy of language has headed. In my opinion, it is far too certain of itself and has exerted far too much influence. The general problem raised by Russell's Paradox of Propositions has yet to be solved, and it must be, if we are to proceed. Kripke, who one might well look to, has made no contribution to this issue. Instead, he has focused attention on a special case of the converse of Russell's assumption about the identity of propositions. Russell's assumption, recall, is that if a and b are distinct objects, then propositions about them are distinct. The converse principle that if a and b are identical objects, then propositions about them are the same, is obviously false. "Romeo loves Juliet" does not entail "Juliet loves Romeo," however much she does according to the facts of fiction. But the special case of this known as "Leibniz's Law" has been the focus of much of the philosophy of language of proper names, since Kripke's Naming and Necessity. Let us put that to rest for a while, and look at other issues.[29] [30] [31]
Let me repeat the main point of the foregoing, lest it be misunderstood. Philosophers have taken refuge in the structured propositions view largely because of what I termed above "Soames' complaint." But there is no refuge to be had as of yet since there is no consistent theory of structured propositions (short of the ramified theory of types). King's theory is inconsistent, as is every other one I know of. The underlying fact was observed by Russell more than one hundred years ago, and the issue was studied carefully by Church almost twenty-five years ago. All of the confident theorizing about structured propositions by the SRP group, is thus suspect; and from the point of view of scholarship, it has developed in ignorance of issues it should have been least ignorant of. This is harsh criticism, I know, but these are the facts. The SRP school of the philosophy of language has also developed, it seems, in ignorance of the discussion of contingency and modal logic that took place in the early nineties -- as referenced above. Many issues concerning propositions, now broached by the SRP group -- such as the question whether propositions can have truth values at worlds where they don't exist (if they don't) -- were discussed at length back then.[32]
[1] See Linsky, L., 1992, "The Problem of the Unity of the Proposition," Journal of the History of Philosophy, 30: 243-273.
[2] Stalnaker, R., 1993, Context and Content, Oxford, Oxford University Press.
[3] See, e.g. Lewis, D., 1970, "General Semantics," in Lewis' Philosophical Papers, Volume 1, New York, Oxford University Press.
[4] Barwise, J. & Perry, J., 1983, Situations and Attitudes. Cambridge/Mass.: The MIT Press.
[5] But I know of no one (else) who has suggested that situation theory "go paraconsistent."
[6] See the entries on situation semantics and Montague Grammar in the Stanford Electronic Encyclopedia of Philosophy for fairly up to date accounts. King remarks (p. 6) that the structured propositions view was "influenced by the seminal work of Saul Kripke." But I know of no place where Kripke articulates the view, and given his work on the semantics of modal logic, one would more naturally associate Kripke with the "sets of situations" approach. (In fact, Kripke wrote a paper (unpublished) in which he takes just that approach.) And the characterization of rigidity and related notions in Naming and Necessity is in terms of possible worlds semantics. It is true, however, that in "A Puzzle About Belief" Kripke articulates a view of substitutivity that suggests -- but does not entail -- the structured propositions viewpoint.
[7] See Scott Soames, "Reference, Attitudes, and Content," in Propositions and Attitudes, Nathan Salmon and Scott Soames, eds., Oxford University Press, 1988. See also the other articles by Soames, especially, "Lost Innocence," referenced in the bibliography of this fine collection. No doubt there is further relevant discussion in Soames' more recent work. But I have not studied that as of yet. Soames' argument is clever and important, and I certainly do not mean to disparage it. Soames carefully proves that when a set of situations view is combined with the Millian view of proper names, and such sets of situations are taken to be the objects of propositional attitudes -- belief in particular -- one gets the result that we must attribute certain beliefs to the agent (that are logical consequences of what the agent does believe) from which the agent would clearly dissent. We end up, in particular, attributing to the "Ancients" the belief that 'Hesperus' and 'Phosphorus' are coreferential! But I think the last step of Soames' argument can be blocked by invoking impossible worlds. Moreover, I think there is a very real question whether, even in this case, we can employ a stubborn Church style argument to the effect that the Ancients did in fact believe that 'Hesperus' and 'Phosphorus' are coreferential, even if they would have strongly dissented. Of course, this involves denying Kripke's strong disquotational principle, but I again think that a good case can be made for that. (See Saul Kripke, "A Puzzle About Belief" in Salmon and Soames, (op. cit.).) Let me add that Soames' paper contains a detailed and technically gratifying n-tuple style account of structured propositions and their recursive truth conditions, which Soames attributes to David Kaplan. One might have expected some discussion of this development in King's book; but there is none. In any case, Soames' account is just as vulnerable to the challenge of Appendix B (see below) as is King's.
[8] See Church, A., 1884, "Russell's Theory of Identity of Propositions," in Philosophica Naturalis, 513-522. Kaplan apparently tries to show that possible worlds semantics faces a similar difficulty. (See n29. But Kaplan's argument turns out to be nothing like Russell's.) Russell's argument specifically employs and requires an assumption about structure. Kaplan may be able to show that a diagonal difficulty infects possible worlds semantics, but it won't be quite the same argument as Russell's. (See below.)
[9] Salmon recognizes the problem and is willing to adopt some form of type theory as background to the philosophy of language. (Personal communication.) I have written to Kaplan, asking him if he endorses the ramified theory of types as background to the philosophy of language. But as of this writing, I have received no reply. As far as I can determine, Kripke has never commented on the potential challenge to his own views posed by Appendix B.
[10] Here King provisionally adopts the Russellian view, popular among Millians or Direct Reference theorists, that propositions contain the actual objects, properties, and relations they mention, rather than "modes of presentation" of such.
[11] See Quine's From a Logical Point of View. Of course, Frege took a very different view; but while he is traditionally associated with the Frege-Russell "equivalence class" construction of numbers, recent work has shown that Frege was the first to have discovered the progression known as the finite (von Neumann) ordinals. There are technical and conceptual reasons to favor this progression. It yields a manageable theory of transfinite ordinals, and it is uniquely the progression that results by taking "epsilon images" of sets. (See H. B. Enderton, 1977, The Elements of Set Theory, Academic Press, San Diego, CA.) There may well be an n-tuple view of propositions that has notable advantages over others.
[12] As Salmon formulates the question, following Frege in "On Sense and Reference," it concerns specifically the behavior of proper names. If proper names, as per Russell, Kripke, and Kaplan, contribute only their referents to the content of the proposition, it becomes particularly hard to explain how two propositional attitude reports can differ in truth value and yet differ only in employing distinct coreferential proper names. But I think the more general and pressing question is the one Frege raises in "On Function and Concept." Are the functions x( x - 4) and x2 - 4x different or not? And if not (which is the official answer in mathematics), then … etc.
[13] See A. Urquhart, "The Theory of Types," in The Cambridge Companion to Bertrand Russell, Cambridge University Press, 2003, pp. 286-309. Urquhart seems to take for granted that the correspondence between (p) (p ∈ m ⊃ p) and m must be an onto mapping. But it need not be a bijection. I believe that I have proved that a similar contradiction can be derived for the case of structured attributes. (Unpublished). However, Gregory Landini has informed me that Russell anticipates this paradox of structured attributes in his correspondence with Frege. But I have been unable to verify this as of this date.
[14] Russell ends Principles with the following memorable remarks: "What the complete solution to the difficulty may be, I have not succeeded in discovering; but as it affects the very foundation of reasoning, I earnestly commend the study of it to all students of logic." Over one hundred years later, one can still say "amen!" Russell's own search for a solution led him round and round, until he finally settled on the ramified theory of types. There's a good account of the ramified theory and Russell's search in Urquhart's article. Urquhart notes that the ramified theory is still of interest in predicative mathematics and the philosophy thereof. He also notes that the ramified theory was an inspiration to Gödel in developing his notion of constructible set, and he adds that type theory has received attention in the foundations of programming languages. But as he says, the ramified theory is now generally regarded as a "relic."
[15] See Church (op. cit.). In this paper Church gives an axiomatization of an extended system of simple type theory obtained by adding a binary connective meaning "is the same proposition as" and he gives a formal derivation of the paradox.
[16] As mentioned, Kaplan is reputed to have found a similar diagonal difficulty in possible worlds semantics. So be it. (See below, n29.) But many philosophers have taken refuge in structured propositions because of Soames' complaint. I am asserting that no refuge is to be had as of now.
[17] This sentence, like its historical antecedent 'Theatetus flies', is unnatural in English. In English 'Rebecca swims' means either that Rebecca is a swimmer or, on occasion, that Rebecca can swim (as in 'Look, Rebecca swims!') but it never means simply that Rebecca is swimming. At least these are my intuitions.
[18] King adds two amendments to the theory: one generalizing it to take contexts of use into account, and another to the effect that syntax encodes the "instructions" for determining the truth value of a proposition at a possible world. As source for this claim that syntax "encodes" semantics, King cites Richard, but not any particular work of the latter. I will only say this: The syntax of the languages of formal first order theories certainly does not encode their semantics, or there would be no need for model theory! But I confess that I have been unable to garner from King's discussion just what is meant by the claim that syntax contains such instructions.
[19] One can draw a technical distinction between propositions and properties of the world, as Soames does in the paper cited earlier. But the question then is: why?
[20] For example, David Braun, 1993, "Empty Names," Nous, 27.4: 449-469.
[21] As Church says, quite dramatically, at the end of his article on Appendix B (op. cit.): "If, following the early Russell, we hold that the object of an assertion or a belief is a proposition, and then impose on propositions the strong conditions of identity which this requires, while at the same time undertaking to formulate a logic that will suffice for classical mathematics [and that will suffice, I would add, for the philosophy of language!], we therefore find no alternative except ramified type theory, with axioms of reducibility … ."
[22] As mentioned earlier, I have asked Kaplan directly in an email whether he endorses the ramified theory of types. I have not as of this writing received an answer. I believe that a new solution may be sought by adding axioms on propositions to those of a suitable set theory; but I myself have as yet not worked out the details.
[23] A number of modern theories have succumbed to versions of the Appendix B argument. I believe the original version of Church's logic of sense and denotation is an example, as is Castaneda's guise theory. In some cases, authors were aware of the problem. In particular, Zalta's and Parsons' versions of object theory place restrictions on the existence and identity conditions for objects that serve to avoid the problem.
[24] Plantinga, A., 1978, "The Boethian Comprimise," American Philosophical Quarterly, 15: 129-138.
[25] Prior, A. N., 1957, Time and Modality. Oxford; Clarendon.
[26] Deutsch, H. 1990, "Contingency and Modal Logic," APA edition of Philosophical Studies, 60: 89-102.
[27] Cf. A. Church, Introduction to Mathematical Logic, Princeton University Press, 1956. As Church says, a proposition is "that which two sentences in different languages must have in common in order to be correct translations each of the other."
[28] King claims that propositions are identical that have the same objects and properties at the terminal nodes of the extended LF graph. But this is not at all clear from his book. I cannot find an explicit discussion of the identity conditions for propositions in King's book.
[29] King's appendix on quantification is the most technical part of the book. King attempts to say exactly what propositions are in the context of a language which resembles the language of logic; and he gives a definition of truth at a world for propositions. I have not mastered the details of King's approach, but my impression is that it resembles the Kaplan/Soames account mentioned earlier. There are special problems connected with representing quantification in what is essentially a set theoretical context; but the theory of generalized quantifiers provides a means to do this, and it looks as though both Kaplan/Soames and King exploit this approach or something like it. The operation of "cylindrification" due to Tarski and Henkin, may be another way to go.
[30] After writing the foregoing, I read David Kaplan's article "A Problem in Possible Worlds Semantics" in Armstrong, Asher, and Raffman, eds., 1995, pp. 51-52. Kaplan purports to show that certain "benign" conditions are not in fact satisfiable in possible worlds semantics, and therefore that the latter does not capture all the possibilities -- in much the same sense that finite models do not capture all that is expressible and satisfiable in first-order logic. I do not agree with Kaplan's conclusion. The fact that Kaplan's formula (A) is not satisfiable in an extension, of, say, S5 that allows for quantification over sets of worlds, shows only, once again, and as has been common in logic, that the possibilities are not what we thought they were -- e.g. it was once thought possible to form a set given any condition on objects whatsoever, and that turned out not to be true (by Russell's Paradox). Kaplan's argument is a Cantorian one, but he doesn't give it in his article, claiming to be maxed out on diagonal arguments! In my opinion, that's no excuse for not trying to lead the reader by the hand.
[31] Kaplan's sentence (A), upon examination, actually asserts, in the language of modal logic, that there exists an onto mapping from worlds to propositions (i.e. to sets of worlds). So of course it is not satisfiable. But the existence of this sentence is very interesting and the fact that it exists may have Gödelian consequences.
[32] King assures me (personal communication) that he has known of this work, but had no space to consider it. But I have not seen references to the relevant papers in any of the work by the SRP group with which I am familiar.
