Fixing Frege

The old part of the story is well known. Between 1875 and 1902, Gottlob Frege developed a new system of logic and tried to use this system to provide a new foundation for mathematics. Unfortunately, in 1902 Russell discovered that Frege's system was inconsistent. As a result, Frege was forced to abandon his foundational project, and the mathematical community eventually turned their attention towards alternate sources of foundations: type theory, set theory, etc.

The new part of the story starts in the early 1980s. At that point, several philosophers (independently) noticed that there is a relatively straightforward way of revising Frege's system so as to both avoid Russell's paradox and preserve an essentially Fregean approach to arithmetic. To understand this revised system, we need to start with two principles. First, there's Frege's own Basic Law V. Law V says that the extension of one concept is equal to the extension of another concept if and only if the same objects fall under the two concepts. More formally:

(V) ∀F ∀G [ Ext(F)=Ext(G) ⇔ ∀x ( Fx ↔ Gx ) ]

Second, there's a principle which has come to be known as Hume's Principle (after a rather cryptic remark from the Treatise ). Hume's Principle says that the number of F's is equal to the number of G's if and only if the objects falling under F can be put into a one-to-one correspondence with the objects falling under G.

(HP) ∀F ∀G [ Num(F)=Num(G) ⇔ F ≡ G ]

where F ≡ G symbolizes the existence of a one-to-one correspondence between the F's and the G's.

What people noticed in the early 80s was that, although (V) is the principle which most directly gives rise to Russell's paradox, it plays only a modest role in Frege's own formulation of arithmetic. In particular, Frege uses (V) in giving an initial proof of (HP); but, once (HP) is on the table, (V) largely disappears from his discussion. This leads to an obvious idea: what if we simply dropped (V) from Frege's system and replaced it with (HP)? This would allow for an essentially Fregean derivation of arithmetic, and it would avoid the obvious derivation of Russell's paradox. Indeed, as several authors later proved, the resulting system is equa-consistent with ordinary second-order PA and so is about as "safe" as a second-order system can possibly be.¹

This, then, is the key idea behind the contemporary resurgence of neo-logicism: to find modest modifications of Frege's logical system which will allow us to derive (much of) contemporary mathematics while avoiding the inconsistencies that plagued Frege's original system. John Burgess' new book, Fixing Frege, provides a guided tour through the mathematical side of this project. It's aims are two-fold: 1.) to bring its readers up to speed on the technical work that's been done in the area and 2.) to highlight the different trade-offs that we have to make as we juggle the various philosophical and mathematical goals of neo-logicism (e.g., maximizing the amount of mathematics our system can capture, preserving the philosophical advantages of Frege's original system, remaining faithful to Frege's own derivation of arithmetic, etc.).

Structurally, the book splits into three long chapters. The first provides some background information. It starts by laying out the basic principles of higher-order logic and sketching the peculiarities of Frege's own system. It then shows how one can use this system to derive the Peano axioms from (HP). Next, it explains how we can use axiom (V) to derive Russell's Paradox, and it looks at Russell's own suggestions for avoiding this paradox. Finally it lays out a hierarchy of theories which can be used to measure the mathematical strength of different neo-logicist proposals.

This last item probably deserves a brief explanation, since it's central to the overall organization of the book. Over the last 50-60 years, logicians have developed a fairly precise way of comparing the mathematical strength of different theories (based, very roughly, on the idea that a theory A is stronger than a theory B if theory B can be interpreted in theory A). Burgess starts his presentation by clarifying the relevant notion(s) of interpretation. He then lays out a sequence of increasingly strong "reference" theories to which different neo-logicist proposals can be compared. The sequence starts with Robinson's Q, works up through the primitive recursive hierarchy and the reverse mathematics hierarchy, and ends with large cardinals and second-order versions of set theory. Given this, Burgess' goal is to determine where/how the different neo-logicist proposals fit into this particular hierarchy.²

Chapter two considers predicative modifications of Frege's system—i.e., modifications which keep Frege's axiom (V) but which replace the standard second-order comprehension scheme with predicative forms of that scheme.³ Burgess starts by showing that even the simplest theories of this form have the resources to interpret Robinson's Q, and he explains how we can get exponentiation by allowing two "rounds" of predicative concepts. He then shows that there are sharp bounds on this kind of iteration: no matter how many "rounds" of predicative concepts we allow, we won't get beyond the super-exponential level of the primitive recursive hierarchy. (Hence, the whole predicative approach won't get us beyond the very lowest levels of Burgess' master scale.) Along the way, Burgess provides nice discussions of, e.g., the effects of adding a "there are finitely many x" quantifier to our language, the strength of predicative versions of (HP), and the prospects for Russell-style zig-zag theories.

Chapter three turns to impredicative theories. The motivating result for this chapter is the theorem mentioned at the beginning of this review: second order logic plus (HP) is equivalent to second-order PA. After a brief discussion of this theorem—and of some nice refinements due to Heck, Tennant, Bell and Linnebo—Burgess turns to the question of whether this result can be extended to other parts of mathematics. That is, can we find principles which look somewhat like (HP)—"abstraction principles" to use the technical jargon—which will allow us to generate analysis, topology, set theory, etc.⁴

Now, if we could simply add any old abstraction principles we wanted to our system—in effect, treating abstraction itself as a logically primitive operation—then there wouldn't be a problem here. Unfortunately, this isn't possible. Some abstraction principles are inconsistent (e.g., Frege's Law V!); there are pairs of abstraction principles which are individually consistent but jointly inconsistent; and there are consistent principles which are incompatible with (HP). Further, a result of Heck's shows that there's no way to tell whether a given abstraction principle—or set of such principles—is consistent. Hence, what we really need is a motivated way of determining which abstraction principles to add to our overall system.⁵

Burgess himself examines two ways of determining this. First, he provides a nice overview of Kit Fine's general theory of abstraction—a theory which attempts to give general conditions under which abstraction principles can be safely added to our logic. For those keeping track, Burgess shows that the nth-order general theory of abstraction is equivalent to (n+1)st-order Peano arithmetic. Next, Burgess looks at a series of abstractionist approaches to set theory. The idea here is to find a modified version of (V) which will let us capture a lot of set theory, and to then define other mathematical objects within that set theory (so, we only need to defend the logical status of a small number of set-theoretic abstraction principles). Burgess ends his book with a nice discussion of the relationship between second-order logic and Fregean versions of set theory (and, more generally, of the role that second-order logic plays in the whole neo-logicist program).

This, then, gives a picture of the contents of Burgess' book. Let me close with three, somewhat more-general comments. First, I want to emphasize just how useful this book will be to people working in the area. The results Burgess is discussing were previously scattered across a wide literature, and much of this literature wasn't specifically focussed on neo-logicism. Further, some of the results were pure mathematical folklore (the experts all knew about the results, but neither the results or their proofs had ever appeared in print). So, simply by gathering all this material into one place, Burgess has done a tremendous service to the philosophical community.

Second, Burgess' mathematical exposition is superb. At the local level, individual proofs are extremely clearly presented, both in terms of their specific steps and in terms of their overall conceptual organization. At the more global level, Burgess does a good job of ensuring that the reader is aware of how particular proofs fit into the book's larger architectonic. This avoids the feeling of wading through long pages of unmotivated mathematical detail. It's also a distinct improvement on the journal literature, where considerations of space all-too-often lead authors to focus on the local details of their proofs at the expense of the larger (mathematical) picture. For those just coming to this literature—or even those who simply want a well-organized refresher course—I can't imagine a better place to start than Burgess' new book.

Finally, I do have one caution about this book. Burgess' project is very much a mathematical project. Although Burgess gestures at some of the philosophical issues raised by this mathematics, he doesn't explore such issues in any real depth. Hence, anyone wanting a purely philosophical introduction to contemporary neo-logicism is advised to start elsewhere, and anyone who needs a lot of philosophical motivation to get interested in technical material is advised to put Burgess' book third or fourth on their list of things to read about neo-logicism. For such readers, Burgess' book wouldn't make a very good beginning.⁶

That being said, this caution isn't intended as a criticism. Burgess set out to explain the mathematical side of neo-logicism, and his book succeeds splendidly at this project. Those initially interested in this kind of mathematics will find Burgess' book immediately—and immensely—rewarding. Other philosophers will discover those rewards in their own time.

Footnotes:

¹This is probably the right place for a little bit of bibliographical information. The basic fact that one can derive arithmetic from (HP) plus second order logic goes pretty far back. One can find the idea in [Geach, 1951], [Geach, 1955] and [Parsons, 1965]. That being said, the idea that this derivation provides an adequate foundation for arithmetic seems to be original to Wright in his influential book Frege's Conception of Numbers as Objects, [Wright, 1983]. At any rate, this is the book that really got the contemporary neo-logicist project off and running.

Wright himself didn't prove the consistency of his new system, nor did he track the details of his new version of arithmetic through all the twists and turns of Frege's own texts. Consistency was proved (independently) in [Burgess, 1984], [Hodes, 1984] and [Hazen, 1985], and, some years later, Boolos and Heck provided detailed analyses of the ways Frege's own arguments can be reconstructed in Wright's new system system. See [Heck, 1993] and [Boolos and Heck, 1998].

²Three comments about this are probably in order. First, there's no guarantee that every theory can be nicely located in relation to this hierarchy: it's easy enough to construct artificial examples of theories whose strength is incommensurable with one or more of the elements of the hierarchy. That being said, almost all natural theories do fit into the hierarcy, and this allows researchers to use the hierarchy as a scale for measuring the strength of different theories. In particular, all of the usual neo-logicist theories fit nicely into this scale.

Second, because this scale is structured in terms of interpretability, it provides a rather direct measure of the ability of different theories to capture different kinds of mathematics. If a given theory can capture a certain kind of mathematics, then any stronger theory will also capture that mathematics. So, once we locate a particular neo-logicist theory on this scale, we get a good feel for how much mathematics that theory will enable us to reconstruct.

Finally, the hierarchy just described allows for some pretty fine-grained comparisons of theories. This is something Burgess makes good use of. He's not, for instance, content with showing that (HP) and PA are equivalent in second order logic. He's after more fine-grained results like the following: Π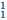 1 1 -Peano arithmetic is mutually interpretable with Π 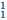1 1 -Frege arithmetic. This level of detail is part of what makes Burgess' book so useful.

³In the simplest case, for instance, we use the scheme: ∃X ∀ x ( Xx ↔ φ(x) ) where φ contains no higher-order quantifiers.

⁴A word on the terminology may be in order here. Abstraction principles get their name because because they introduce abstract objects by means of equivalence relations on concepts. So, for example, (HP) introduces numbers as abstracts for the equivalence relation "being in on-to-one correspondence," and (V) introduces extensions as abstracts for the relation "applying to the same objects." More generally, let ≈ be any equivalence relation on concepts. An abstraction principle for ≈ would have the form: ∀F ∀G [ Abst(F)=Abst(G) ⇔ F ≈ G ].

⁵This can be tricky even in the mathematical context, but it's a real problem in the philosophical context. Neo-logicist philosophers want to claim that some abstraction principles—like (HP)—are actually fundamental principles of logic. This means that they need a principled way of distinguishing good abstraction principles from bad ones. For mathematical purposes, of course, we can avoid this issue of principle by simply doing things piecemeal, adding new abstraction principles as we see fit and proving consistency any way we want. This seems less plausible as an approach to the foundations of mathematics.

⁶Readers looking for a more purely philosophical introduction to the subject are advised to begin with Fraser McBride's nice survey in [McBride, 2003]. They should then work through some of the papers in [Hale and Wright, 2001].

References

[Boolos and Heck, 1998]: Boolos, G. and Heck, R. (1998). Die Grundlagen der Arithmetik § § 82-83. In Boolos, G., Logic, Logic, Logic, pages 315-338. Harvard, Cambridge.
[Burgess, 1984]: Burgess, J. (1984). Review of [Wright, 1983]. Philosophical Review, 93:638-40.
[Geach, 1951]: Geach, P. (1951). Frege's Grundlagen . Philosophical Review, 60:535-544.
[Geach, 1955]: Geach, P. (1955). Class and concept. Philosophical Review, 64:561-570.
[Hale and Wright, 2001]: Hale, B. and Wright, C. (2001). The Reason's Proper Study. Oxford, Oxford.
[Hazen, 1985]: Hazen, A. (1985). Review of [Wright, 1983]. Australasian Journal of Philosophy, 63:251-254.
[Heck, 1993]: Heck, R. (1993). The development of arithmetic in Frege's Grundgeetze der Arithmetic . The Journal of Symbolic Logic, 58:579-601.
[Hodes, 1984]: Hodes, H. (1984). Logicism and the ontological commitments of arithmetic. The Journal of Philosophy, 81:123-149.
[McBride, 2003]: McBride, F. (2003). Speaking with shadows: A study of neo-logicism. British Journal for the Philosophy of Science, 54:103-163.
[Parsons, 1965]: Parsons, C. (1965). Frege's theory of number. In Black, M., editor, Philosophy in America, pages 180-203. Cornell, Ithaca.
[Wright, 1983]: Wright, C. (1983). Frege's Conception of Numbers as Objects. Aberdeen University Press, Aberdeen.