Fitch (1963) published a proof of an entailment p→◊Kp |- p→Kp that Hart and McGinn (1976) take to be a reductio of anti-realism.[1] In response, most of the literature has attempted to construct, or undermine, defences of anti-realism: "restrictionists" argue that the reductio fails because anti-realism is not committed to p→◊Kp in full generality, while "revisionists" point out that both the classical logic employed in the "proof," and the classical semantics on which even such theses as p→¬¬Kp appear absurd, have been rejected on independent grounds.[2] Despite devoting chs. 3 and 5, respectively, to these defences, and ch.2 to anti-realism's motivation, Kvanvig's central thesis is that these responses miss the point because the proof is a genuine paradox that ought to trouble realists and anti-realists alike: since the converse entailment clearly holds, the proof seems to render p→◊Kp and p→Kp logically equivalent, thereby undermining a distinction between "possible and actual knowledge" (p.2) and "some of our deepest modal convictions" (p.53); to escape paradox, we must either restore the distinction or render its loss "palatable by [means of] a semantic explanation" (p.53).[3]
Kvanvig deems another response first investigated in Williamson (1993), which amounts to the rejection of one of the two epistemic principles on which the proof relies, more germane, but in ch.4 he argues that the case against it is "airtight" (p. 121). Concluding that a different approach is required, in ch.6 he tries to defend, from objections by Williamson (2000), a proposal he had made ten years earlier[4].
Kvanvig's idea is that provided we adopt a "neo-Russellian view of quantification" the paradox turns on "a mistake of illicitly substituting into an intensional context" (p.156). Since the proof is conducted in propositional (epistemic) modal logic, this idea might puzzle. But a quantifier is implicit in Kp, which is more perspicuously written ∃xK(x,p), and Kvanvig takes another to be implicit in the sequent p→◊∃xK(x,p) |- p→∃xK(x,p), which he reads as ∀p(p→◊∃xK(x,p)) |- ∀p(p→∃xK(x,p)). The upshot is that the first step in the original proof -- the substitution of q&¬Kq in p→◊∃xK(x,p) -- amounts to substituting a quantificational sentence q&¬∃yK(y,q) for a variable that first falls within the scope of two intensional operators, ◊ and K, and is then bound by ∀.
In effect, Kvanvig poses a dilemma for this substitution. The quantifiers are either non-possibilist or possibilist. If they are non-possibilist, then by the neo-Russellian theory of quantification, q&¬∃yK(y,q) is "modally indexical," and the substitution is illegitimate. If they are possibilist, the substitution is legitimate but the proof is no longer paradoxical because ∀p(p→◊∃xK(x,p)) and ∀p(p→∃xK(x,p)) then "say, in essence, the same thing" (p.172). Neither horn is developed in a convincing manner, however. In showing this, I will follow Kvanvig's practice of employing italicisations to express possibilist quantifiers.
Let us begin with the second horn. Prima facie, since 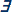 xK(x,p) occurs within the scope of a possibility operator in∀p(p→◊∃xK(x,p)), but not in ∀p(p→∃xK(x,p)), it is incorrect to hold that in essence the two formulae say the same thing: ∀p(p→∃xK(x,p)) says each possible proposition is such that, if it is true then some possible person knows as much, whereas ∀p(p→◊∃xK(x,p)) says every possible proposition is such that, if it is true then possibly, some possible person knows as much. Kvanvig attempts to rebut this observation, which Williamson (2000: 288) had made earlier, by remarking that there is no logical distinction between what possible beings know, and what, possibly, possible beings know: "[∀p(p→∃xK(x,p))] … involves a concept of possibility preceding the knowledge operator, since the concept of possibility is contained within the quantifiers themselves" (p. 177), and "◊◊p -||- ◊p" (p.173).
xK(x,p) occurs within the scope of a possibility operator in∀p(p→◊∃xK(x,p)), but not in ∀p(p→∃xK(x,p)), it is incorrect to hold that in essence the two formulae say the same thing: ∀p(p→∃xK(x,p)) says each possible proposition is such that, if it is true then some possible person knows as much, whereas ∀p(p→◊∃xK(x,p)) says every possible proposition is such that, if it is true then possibly, some possible person knows as much. Kvanvig attempts to rebut this observation, which Williamson (2000: 288) had made earlier, by remarking that there is no logical distinction between what possible beings know, and what, possibly, possible beings know: "[∀p(p→∃xK(x,p))] … involves a concept of possibility preceding the knowledge operator, since the concept of possibility is contained within the quantifiers themselves" (p. 177), and "◊◊p -||- ◊p" (p.173).
Unfortunately, this attempted rebuttal is vitiated by controversial presuppositions Kvanvig chooses not to make explicit. Presumably, he has in mind some such reduction of possibilist discourse as the one proposed by Fine (2003). On it, to a first approximation, ∃xφ is defined as ◊∃xφ, in which case ∀xφ becomes ¬◊∃x¬φ(i.e. ∀ xφ), ∀p(p→◊∃xK(x,p)) becomes ∀ p(p→◊◊∃xK(x,p)), and since ∀p(p→∃xK(x,p)) becomes ∀p(p→◊∃xK(x,p)) the concept of possibility is indeed "contained" in the possibilist quantifiers in such a way that K falls within the scope of ◊ in ∃xK(x,p)). But whatever he has in mind, Williamson's (1998, 1999) account of the possibilist quantifiers is quite different, and on it the concept of possibility is not contained within them. In Williamson's view, possibilist quantification is just non-possibilist quantification freed from actualist restriction; it reaches objects, such as merely possible people, typical restrictions exclude.[5] From this viewpoint, Kvanvig's remark that when a quantifier ranges over objects that include merely possible people it "contains" the concept of possibility, is as absurd as the remark that because Bill brought a tomato for lunch the concept "red" is contained in the quantifier used to assert that something on Bill's desk is edible. The best that could be said of the second horn of the dilemma Kvanvig poses, therefore, is that it begs the question: it does not address the arguments in favour of an influential account of possibilist quantification with which it is incompatible.
Let us turn to the first horn. In it, the existential quantifier is taken to be non-possibilist, and on this basis the claim is made that (q&¬∃yK(y,q))→◊∃xK(x,(q&¬∃yK(y,q))) is not a legitimate instance of ∀p(p→◊∃xK(x,p)) because: (i) the correct account of quantification is "neo-Russellian," in the sense that a sentence "'∀xFx' expresses a proposition that has as constituents being F and the domain of quantification" (p.171, my underlining); (ii) on a "neo-Russellian" account, "[non-possibilist] quantified sentences are modally indexical with regard to the propositions they express," in that "if the very same [such] sentence with the very same meaning is asserted in a different possible world with a different domain, a different proposition is expressed" (p.157); and (iii) in order "for the substitution [of a formula for a propositional variable within the scope of ◊] to be legitimate, the formula would have to be modally non-indexical" (p.162). Only (the underlying thought behind) (ii) is true, however.[6] In reverse order, I will show that (i) and (iii) are false.
Let a sentence S be "O-rigid" iff it expresses the same proposition inside O's scope as it expresses outside it. When ∀ binds a variable that occurs both inside and outside the scope of an operator O, a sentence S which, outside O's scope, expresses a proposition in ∀'s domain, is legitimately substituted for the variable so as to obtain an instance of the universal generalisation, iff S is O-rigid. So (iii) is true only if no modally indexical sentence is ◊-rigid. Some modally indexical sentences are ◊-rigid, however. For example, the modally indexical sentence "that man is bald" is ◊-rigid: at a given context of utterance, it expresses the same proposition both inside and outside the scope of ◊. In particular, the sentence "that man is bald → ◊¬(that man is bald)" expresses an instance of the (unrestrictedly) universal generalisation ∀p(p→◊¬p). So (iii) is false.
Curiously, Kvanvig provides a second illustration of this point when he says, pace (iii), that "the contingency of the proposition expressed by uttering 'I am here now' can be expressed by uttering in the same context 'it is possible that I am not here now'" (p.192). Since he insists that "[this] does not affect the point on behalf of the neo-Russellian view of quantification … [t]he phrase 'it is possible that' forces a change of context when it prefaces a quantified sentence on the neo-Russellian view, but not otherwise" (p.192),[7] charity inclines one to suppose that (iii) is the infelicitous expression of some such thought as this: for there to be a guarantee that the substitution [of a formula for a propositional variable within the scope of ◊] is legitimate, the formula has to be modally non-indexical; to ascertain whether the substitution of a modally indexical formula is legitimate, we must proceed case by case.[8]
Direct examination of the case at issue reveals Kvanvig's basic idea that the proof of ∀p(p→◊∃xK(x,p)) |- ∀p(p→∃xK(x,p)) fails because the claim that non-possibilist quantifiers are not ◊-rigid is untenable. Consider the following assertion: "I did not know that everything in my pocket is such that, if it is a coin it is a penny, but had there been no coins in my pocket, and I had found out, I could have deduced as much." This is a straightforward account of how something I claim not to have known is such that, had certain counterfactual circumstances obtained, I could have deduced it. But this is only so if "as much" is anaphoric for the sentence "everything in my pocket is such that, if it is a coin it is a penny," and the quantifier this sentence involves is rigid with respect to both modalities within whose scope "as much" falls. One reason Kvanvig misses this is that he seems unable to address the matter directly: when called to do so, he slips into discussing modal indexicality and the neo-Russellian view.[9]
The question as to whether q&¬∃yK(y,q) is ◊-rigid is trivial unless pertinent sentences of this form are modally indexical. Kvanvig takes this matter to rest on whether, as on the neo-Russellian view, quantification induces modal indexicality.[10] Although he introduces this view as if it follows from the doctrine of contextual domain-restriction, i.e. according to which the semantics of non-possibilist quantifiers embodies a domain-determining parameter set by context,[11] the two issues are independent. In particular, what Kvanvig calls the alternative "Fregean" view can accommodate contextually restricted quantification. Since the Fregean view holds that "the existential quantifier in the sentence '∃xφx' contributes, to the proposition expressed, the second-order property that the property expressed by 'φ' has at least one instance" (p.176), it has a contextualised variant according to which, at a context of utterance c, the existential quantifier in the sentence '∃xφx' contributes, to the proposition expressed at c, the second-order property that the property expressed by 'φ' has at least one instance having the property δ(u), i.e. where δ is a function from contexts of utterance to properties.[12]
Nor do Kvanvig's attempts to argue for the neo-Russellian view from specific examples succeed. He describes cases in which, implicitly, a proposition expressed by a sentence of the form "∀x(Fx→Gx)" is known, and then proceeds to argue that in a certain counterfactual situation, knowledge that is expressed there by uttering the sentence is not knowledge of the same proposition, either because, unlike in the actual situation, there are no F's (p.160), or because none of the F's overlap with the actual objects (p.197). In the latter case he says "suppose we have two worlds, one actual and one possible. In the first world are objects a, b, and c; in the second world are objects d, e, and f. All of these objects are P, but in the first world, no one knows that everything is P. In the second world, someone does know that everything is P." He then asks "Does this detail show that what is unknown in the first world is in fact knowable?" His answer is that "it does not, because what is known in the second world doesn't appropriately characterize what is unknown in the first world." This argument is an equivocation, however: the characterisation is only inappropriate, if, as is all too easy, we presume what is unknown in the first world is that a, b, and c are P, or what is known in the second world is that d, e, and f are P. One way to see this is to redescribe the case so as to preclude equivocation. Suppose that in w everything is P and no one knows it, but that in w* someone knows that everything is P. In striking contrast to the demonstrative analogue, it would be quite inappropriate to respond to the question "Is what is unknown in w known in w*?" by saying "The propositions unknown in w and known in w* have not been specified in a way that permits an answer, since we haven't been told whether w has the same domain as w*."[13]
A second demonstrative analogue provides another refutation of the neo-Russellian view. The main ground for the thesis that demonstrative thought is object-involving is the intuitiveness of the supposition that when an actual demonstrative thought is evaluated at a counterfactual circumstance, the evaluation turns on how things are, in that circumstance, with the object actually demonstrated. In the case of quantification, however, intuition runs in the opposite direction. Assume domain-restriction, and consider the proposition Q expressed when, at a party at which the people in view are enjoying themselves, I say "Everyone is having a good time." Suppose this assertion is false because Sally is sulking in a dark corner. Without knowing whether Sally likes to skate I can know that Q would have been true, all things being equal, had she accepted Jim's invitation to go ice-skating instead: how things are with her is irrelevant to Q's evaluation in circumstances in which she is not at the party.
Ultimately, Kvanvig's main argument for the neo-Russellian view is that it serves to block the proof that p→◊Kp entails p→Kp. But this argument presupposes his central thesis that the entailment is "paradoxical," and this thesis is false: there is nothing paradoxical in the observation that there is no possible circumstance in which someone might assert an unrestrictedly quantified sentence of the form "q but no one ever knows it" so as to express knowledge of a proposition thereby expressed, and this observation provides an explanation of why p→◊Kp entails p→Kp. Moreover, the argument is self-defeating: to say that the entailment fails when it involves non-possibilist quantifiers for which the neo-Russellian view is correct is to admit that it holds when it involves non-possibilist quantifiers for which the Fregean view is correct, and there is no mileage in maintaining either that Fregean quantification is unintelligible, or that when Fregean quantifiers are utilised the entailment is no longer paradoxical.[14]
Hart and McGinn's (1976) claim that anti-realism is undermined by the entailment p→◊Kp |- p→Kp has occasioned interesting ideas in the restrictionist and revisionist literature even realists should know about. Although his attempt to block the proof is untenable, and in some respects careless, Kvanvig's book serves as a useful introduction to them. Regrettably, ch.6 is littered with typographical errors, some of which make the text difficult to follow.[15]
References
D. Edgington (1985), "The paradox of knowability," Mind 94, 557-68.
K. Fine (2003), "The problem of possibilia," pp.161-79 of M. Loux and D. Zimmerman (eds.), The Oxford Handbook of Metaphysics, Oxford University Press: Oxford.
F.B. Fitch (1963), "A logical analysis of some value concepts," Journal of Symbolic Logic 28, 135-42.
W.D. Hart and C. McGinn (1976), "Knowledge and necessity," Journal of Philosophical Logic 5, 205-8.
J. Kvanvig (1995), "The knowability paradox and the prospects for anti-realism," Nous 29, 481-500.
P. Percival (1991), "Knowability, actuality, and the metaphysics of context-dependence," Australasian Journal of Philosophy 69, 82-97.
T. Williamson (1998), "Bare possibilia," Erkenntnis 48, 257-73.
T. Williamson (1999), "Truthmakers and the converse Barcan Formula," Dialectica 53, 253-70.
T. Williamson (2000), Knowledge and its Limits, Oxford University Press: Oxford.
[1] An anonymous referee reported the proof to Fitch, as did another to Hart and McGinn. The latter read "K" as "it is known that."
[2] Rejecting double negation elimination, intuitionists deny the step from p→¬¬Kp to p→Kp.
[3] Kvanvig denies that intuitionistic revisionism addresses the paradox, on the grounds that it regains "the … distinction between known and knowable truth [at the expense of] … a lost distinction between unknown and unknowable truth" (p. 201). This position is puzzling. As Alan Weir pointed out to me, it begs the question against those intuitionists who on independent grounds reject as incoherent the notion of an unknowable truth.
[4] Kvanvig (1995: 493-6).
[5] This account has two variants, depending on whether the modality in e.g. "(merely) possible person" is taken to be predicative or attributive. The classical variant favours the former: it takes an object that is a merely possible person to be a person who is merely possible. The non-classical variant Williamson advocates favours the latter: it takes an object that is a merely possible person to be a non-person that is merely potentially a person.
[6] For (ii) to express a truth, in "if the very same [such] sentence … is asserted in a different possible world with a different domain," the phrase "different domain" must pertain to the respective domains over which the quantifiers range at the two contexts of utterance, not to the respective domains of the possible worlds in which the utterances occur.
[7] In insisting this much, Kvanvig also contradicts his earlier claim (p. 159) that on the neo-Russellian view, the sequent ◊∀x(Sx→Fx), Sa |- ◊Fa is correct.
[8] On this interpretation Kvanvig takes the neo-Russellian view of quantification to be a crucial first step in dispelling the knowability paradox: he takes it to establish the epistemic possibility that the quantifiers are not ◊-rigid. The interpretation is difficult to sustain, however, since he consistently writes as if his proposal stands or falls with the neo-Russellian view itself. For example, he says that one consideration in this view's favour is that it blocks the knowability paradox. Were the interpretation correct, however, one would have expected him to say that the thesis that the quantifiers are not ◊-rigid is supported by the fact that it blocks the paradox; that this fact in turn supports the claim that a sentence of the form q&¬∃yK(y,q) is modally indexical; and that this claim in turn supports the neo-Russellian view of quantification. The fact is that Kvanvig does not clearly demarcate the following claims regarding quantifiers: they are object-involving (in the neo-Russellian sense); they are modally indexical (in his sense); they are not ◊-rigid. We will soon see that on occasion he runs them together with the further claim that non-possibilist quantifiers are subject to contextually determined domain-restriction.
[9] For example, see p.162.
[10] Although Kvanvig discusses Edgington's (1985) suggestion that non-actual knowledge of a proposition expressed by "q&¬∃yK(y,q)" is best conceptualised by analogy with non-present knowledge of, e.g., the proposition presently expressed by the sentence "the number of hairs on Tony Blair's head is even and no one knows it," he does not investigate the thought that q&¬∃yK(y,q) is modally indexical in just the way that this sentence is temporally indexical. (See Percival (1991) for discussion.)
[11] See pp.156-7, and in particular the remark that "if we take [the quantifier in question] to be a restricted quantifier, then the quantifier behaves in an indexical fashion."
[12] Subsequently (p. 171), Kvanvig acknowledges that the neo-Russellian view is compatible with the view that non-possibilist quantifiers are unrestricted.
[13] Suppose that in w, that is red, and no one knows it, but that in w it is known that this is red. It would not be inappropriate to respond to the question "Is what is unknown in w known in w*?" by saying "The propositions unknown in w and known in w* have not been specified in a way that permits an answer, since we haven't been told whether the demonstratives have the same reference." In fact, this response is obligatory.
[14] Here, by "Fregean" I mean "not object-involving." Kvanvig's presumption that the entailment holds on the Fregean view exposes the weaknesses in his characterisation of it as holding that "the existential quantifier in the sentence '∃xφx' contributes, to the proposition expressed, the second-order property that the property expressed by 'f' has at least one instance." A first-order quantifier -- "at least one instance" -- is involved in this second-order property, and if it is interpreted in a neo-Russellian manner the property will be object-involving (i.e. in the way in which, e.g., the property of being married to Tony Blair is). In that case, contrary to Kvanvig's intentions, the Fregean view will also hold that the non-possibilist quantifier induces modal indexicality. (Of course, the difficulty of giving a non-circular explanation of quantification does not tell against the intelligibility of quantifiers that are not object-involving.)
