Socratic Epistemology has been awaited with anticipation. Jaakko Hintikka has surely committed his thoughts on epistemology to print many times before but this is the first time Hintikka literally pieces together the new story on how epistemic logic hooks up with the more classical epistemological issues. The book offers novel and provocative views on a wide variety of classics ranging from the notions of knowledge and belief, the apriori, abduction, inference and explanation just to mention a few. While examining these key concepts Hintikka simultaneously takes critical stock of contemporary epistemology. The book is a collection of ten very engaging, erudite and sometimes quite polemical essays, some of which are new, and some of which have been published before but have been revised for this volume.
Partitioning
Ever since the early 1960's, Hintikka has been emphasizing the significance of the process of partitioning possible scenarios while ascribing propositional attitudes. The process features as the key unifying concept running all the way through Socratic Epistemology, culminating in his general understanding of inquiry, decision-making and action.
The point of partitioning is inherent in Hintikka's seminal book Knowledge and Belief: An Introduction to the Logic of the Two Notions (1962). In 'Semantics for Propositional Attitudes' (1969) his case for partitioning reaches an abundantly clear formulation:
My basic assumption (slightly oversimplified) is that an attribution of any propositional attitude to the person in question involves a division of all possible worlds (more precisely, all the worlds which we can distinguish in the part of language we use in making the attribution) into two classes: into those possible worlds which are in accordance with the attitude in question and into those worlds which are incompatible with it. (Hintikka 1969, p. 91)[1]
This formulation is relativized to knowledge (its use and the relation to epistemic logic) in the first paper of Socratic Epistemology with the initially puzzling and provocative title 'Epistemology Without Knowledge and Without Belief':
In order to use my knowledge, I must know which possibilities it rules out. In other words, any one scenario must therefore be either incompatible or compatible with what I know, for I am either entitled or not entitled to disregard it. Thus the totality of incompatible scenarios determines what I know and what I do not know, and vice versa. In principle, all that there is to logic of knowledge is this dichotomy between epistemically impossible and epistemically possible scenarios. (p. 12)
This partitioning is also mirrored in the, by now canonical, semantic interpretation of the epistemic and doxastic operators in epistemic logic; for an agent a and an arbitrary proposition p, Ka p reads: in all possible scenarios compatible with what a knows it is the case that p, and similarly for the doxastic operator Ba p.
From here, Hintikka takes a further step. As already noted, any attitude requires partitioning, and there is an epistemological concept which is much more central to epistemology than, say, knowledge and belief -- and that concept is information. The reason is that information
· is modularizable in knowledge, belief and other attitudes,
· is the goal of inquiry, and
· is the stuff decisions and actions are based upon.
From Knowledge to Information
The concept of knowledge has come under attack in recent years. Some say that it is an overrated concept for deliberation, decision and action and that one may make do with some measure of opinion as long as the measure is strong enough. Although Hintikka has been one of the pioneers in bringing knowledge to the attention of mainstream, and especially formal, epistemologists (ranging from logicians to computer scientists and information technologists) he is also one of the formal philosophers to criticize it the most.
The point is not that knowledge is overrated as some Bayesians may have it -- it is just the wrong concept to place front and center in epistemology. That's the way of the past, that's the way of the present, but it's not the way of the future if Hintikka has his way with replacing the concepts of knowledge, belief, etc. with the concept of information, or 'information range' as van Benthem and Martinez have recently called it (van Benthem & Martinez 2008).
Knowledge is obviously a guide to action, but so are attitudes like certainty, belief, conviction, etc. in different degrees and with different constraints enforced for their satisfaction. Additionally, the content of a propositional attitude can be specified independently of discrepancies between the different attitudes -- an insight dating back to Husserl’s separation of the noematic Sinn from the thetic ingredient of a noema.
If knowledge, certainty, belief and conviction are attitudes towards propositional content, so is doubt, and the content of a doubtful attitude is just as specifiable as the content of any epistemically positive attitude. Being skeptical requires information; otherwise there is little to be skeptical about. And being a skeptic is in turn cultivated by doubt as to how the information in question is acquired. That's all there is to say about skepticism -- its presupposition is inquiry, so why all the fuss over the past many years?
The very same goes for the remaining attitudes: 'knowledge' is a label for a particular way of having acquired information; 'belief' is likewise an 'achievement' word wired to a different set of criteria related to when the agent is ready to act on the information in question. In sum, knowledge, belief, certainty, conviction, etc. are all derivatives with information as the basis.
The idea seems to be this: A particular attitude is extracted from the general information partition in terms of the additional constraints enforced for the attitude to materialize. When the knowledge attitude is taken to entail infallibility, then all possibilities of error are excluded relative to the set of possibilities in accordance with the attitude. Certainty, say, does not exclude all possibilities of error, but most of them (a probability measure may come into play here as Hintikka notes) relative to the set of worlds in accordance with the attitude, and so forth for belief, conviction and the other attitudes all they way down to doubt which excludes almost no possibilities of error. Knowledge is modularized information, and that goes for all the other attitudes as well (Figure 1).
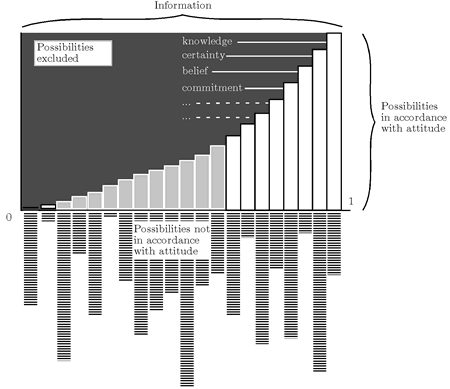
Figure 1: Information, partitions, excluded possibilities and attitudes.
Inquiry, Decision and Action
Information is acquired via interrogative inquiry. New information is the result of answers to questions that an inquirer directs to some suitable source of information ('Who Has Kidnapped the Concept of Information?').
And now things are coming together, because in this inquiry process epistemic logic plays a paramount role in conjunction with its close ally game theory:
Another main requirement that can be addressed to the interrogative approach and indeed to the theory of any goal-directed activity is that it must do justice to the strategic aspects of inquiry. This requirement can be handled most naturally by doing what Plato already did to the Socratic elenchus and by construing knowledge-seeking by questioning as a game that pits the questioner against the answerer. Then the study of those strategies of knowledge acquisition becomes another application of the mathematical theory of games, which perhaps ought to be called strategy theory in the first place. (p. 13)
Epistemic logic is really a logic of questions and answers and the search for the best questions to ask ('A Second-Generation Epistemic Logic and Its General Significance,' The Place of the Apriori in Epistemology'). In this new setting, epistemic logic augmented with an independence-friendly logic constitute the basis for an interrogative theory of inquiry.[2] Answers to questions are in essence requests for knowledge, information or epistemic imperatives. Hintikka's approach rests on the recognition that questions are essentially epistemic, insofar as they express epistemic aims. A question's epistemic aim can be presented as a statement specifying the epistemic state which the answer will bring about; the desideratum of a particular question.
Hintikka understands his interrogative model as a game against nature, or against any source of answers to queries ('Presuppositions and Other Limitations of Inquiry'). He distinguishes two different kinds of rules or principles characteristic of a game. The definitory rules define the game. In a game of chess, for instance, the definitory rules tell us which moves are permitted and which not, what checkmate, castling, etc. mean, and so on. If a player makes a move not allowed by the definitory rules, say by moving a pawn three spaces forward, it is not a chess move and the player must take it back. One may thus describe the definitory rules of any game or rule-governed, goal-oriented activity. However, knowing the definitory rules of a game does not mean you know how to play. One must also know what Hintikka calls the strategic rules (or principles) of a game. In chess, for instance, you must plan your moves, select the best course of action, make judgments as to which moves will serve you better than others, and so on. These rules are not merely heuristic. They can be formulated as precisely as the definitory rules. This is well explained by the crucial role of complete strategies in von Neumann's game theory.
The result of applying Hintikka's distinction to the interrogative games of inquiry reveals the following: The standard rules of an interrogative game, the rules for logical inference moves, as well as interrogative moves, are definitory. They say little to nothing about what to do in a logical or epistemological game. The rules for making both logical inference moves and interrogative moves merely define the game. For example, the rules of inference in deductive logic are neither descriptive nor prescriptive but merely permissive, in so far as they do not tell us which particular inference or set of inferences we should draw from a given number of potential premises ('Abduction -- Inference, Conjecture, or an Answer to a Question?', 'Logical Explanations'). What is needed, if inquiry is going to be successful, is more than the definitory rules of inquiry. Strategic rules are needed. Indeed, the better the strategic rules, the better our inquiry. The best player in a game of inquiry is the player with the best strategy, which corresponds in game theory to what happens where values, i.e., utilities, are associated not with moves themselves but, rather, with combinations of strategies, as in von Neumann's game theoretical notion of a complete strategy.
Piecing it Together
This is roughly how all the epistemological ends meet in Hintikka's new Socratic Epistemology. Besides the program outlined above there are also a couple of papers concerned with applications -- one written jointly with John Symons on how epistemic logic may be used to clarify and précis certain problems related to visual identification in neuroscience, and a short, crisp piece criticizing the 'theory of cognitive fallacies' proposed by Tversky and Kahneman.
Socratic Epistemology makes for an extremely enjoyable read -- it is as erudite as it is engaging with the lively polemical touch of Hintikka's pen. Since it is a collection of papers rather than a monograph there is a bit too much repetition in terms of basic machinery re-introduced in many of the papers. On top of that, it is a mereological exercise to piece the over-all epistemological view together, unless one is really familiar with the Hintikkian realm of thought. However, the first paper, 'Epistemology Without Knowledge and Without Belief', does actually serve to some extent as a guide to the rest of the papers in the volume.
Socratic Epistemology has been awaited with anticipation, and Hintikka fully delivers. This is one truly original piece of epistemology and mandatory reading for mainstream and formal epistemologists alike.
References
Arló-Costa, H. (2006). Review of V.F. Hendricks's Mainstream and Formal Epistemology, Notre Dame Philosophical Review, October 2006. http://ndpr.nd.edu/review.cfm?id=7044.
Benthem J.v. & Martinez, M. (2008). 'The Stories of Logic and Information', forthcoming in Handbook of the Philosophy of Information.
Hendricks, V.F. (2006). Mainstream and Formal Epistemology. New York: Cambridge University Press.
Hintikka, J. (1962). Knowledge and Belief: An Introduction to the Logic of the Two Notions. Cornell: Cornell University Press, 1962. Reprinted in 2005 by King's College Publications, London.
Hintikka, J. (1969). 'Semantics for Propositional Attitudes', in Models for Modalities. Dordrecht: D. Reidel Publishing Company: 87-111.
[1] In 'A Second-Generation Epistemic Logic and Its General Significance' from the current volume, Hintikka describes the philosophers' usage of 'possible worlds' as a symptom of intellectual megalomania. Already in Knowledge and Belief, Hintikka used 'model sets' (as formal counterparts to (partial) descriptions of state of affairs) which are not complete linguistic descriptions of possible worlds. The nature of the 'space of options,' as Hintikka calls it, is of acute importance for many a central epistemological issue including the nature of the accessibility relation built in the model and thus also for the nature of the forcing relation responsible for partitioning (Arló-Costa 2006).
